Let A and B denote random population samples from different populations, µ denote the average function, and, σ² denote the variance function:
σ²(A - B) = µ(((A - B) - µ(A - B))²)
σ²(A - B) = µ(((A - µ(A)) - (B - µ(B)))²)
σ²(A - B) = σ²(A) + σ²(B) - µ(2(A - µ(A))(B - µ(B)))
Since µ(2(A - µ(A))(B - µ(B))) = µ(2) µ(A - µ(A)) µ(B - µ(B)), σ²(A - B) = σ²(A) + σ²(B).
If the probability distribution of a population is P(n) where P(0) = 1 - p, P(1) = p and P(n) = 0 otherwise, for some p, then that probability distribution is referred to as a Bernoulli distribution. The population average is p and the population variance is p (1 - p).
Mathematicians tend to use the term average. Statisticians tend to use the term mean. They both correspond to the same formula.
Data frames are data structures similar to SQL tables.
Decision tree based models use flowcharts and therefore do not require scaled input data.
The central limit theorem states that, for sets of random population sample averages, with sample size N, the following are true:
Frequency distributions are normally distributed.
Averages are approximately equal to the population average.
Standard deviations are approximately equal to the population standard deviation divided by √N.
Approximation accuracies improve as N increases.
The population standard deviation divided by √N is referred to as the standard error of the average. All this is true even for populations that do not correspond to normal distributions!
The following is the frequency distribution of 20,000 random population sample averages, with sample size 2000, from a population with a probability distribution
of P(n) = 0.41703239142 / (n - 9) for 10 ≤ n ≤ 20 and 0 otherwise:
The population has an average of 13.17032. The population and sample size have a standard error of 0.06177. The random population sample averages have an average of 13.17030 and a standard deviation of 0.06192.
The normal distribution function is the following where z(x, μ, σ) = (x - μ) / σ:
Frequency distributions described by this function are referred to as normal distributions.
Decreasing classification model thresholds decreases precisions and increases recalls. PR (precision recall) curves show precisions and recalls as thresholds are decreased. Greater accuracies imply greater areas under PR curves.
Binary classification models can have two recalls. If one recall is referred to as the true positive rate, one minus the other recall is referred to as the false positive rate. Decreasing binary classification model thresholds increases both true and false positive rates. ROC (receiver operating characteristic) curves show true and false positive rates as thresholds are decreased. Greater accuracies imply greater areas under ROC curves.
Percentiles are numbers that correspond to divisions of sets of numbers containing given percentages. For example, 90% of elements in a set of numbers are smaller than the ninetieth percentile.
Interquartile ranges are the differences between the largest and smallest quartiles.
Probabilities for random forest classification models equal the decision tree class percentages.
Ranges of decision tree based models equal the corresponding training data output value ranges.
The bias variance problem corresponds to the problem of needing to somehow avoid both underfitting and overfitting when creating models. Useful techniques include increasing the amount of training data and cross validation.
Language models are machine learning models that predict words likely to follow given word sequences. Predictions depend on the textual training data used to build the models. Applications include summarization, translation and chatbots.
Word embeddings are vector representations of words such that similar meanings imply similar vectors. Word embeddings are built by assuming meaning corresponds to context. Two word embedding methods are Word2vec and GloVe.
Transformers are deep learning sequence models that rely on the attention mechanism to determine sequence element relationships. Sequence examples include text, audio and video. Application examples include translation and transcription.
AlexNet is a famous deep learning convolutional neural network image classifier developed by Alex Krizhevsky, Ilya Sutskever and Geoffrey Hinton. It spurred lots of interest in computer vision and deep learning. The following uses a modified PyTorch implementation of AlexNet, and a graphic processing unit, to implement an image classifier using the CIFAR 10 (Canadian Institute For Advanced Research) dataset:
import torch
import torch.nn
import CIFAR_10
LEARN_RATE = 0.001
MOMENTUM = 0.9
BATCH_SIZE = 64
N_EPOCHS = 9
ERROR = torch.nn.CrossEntropyLoss()
CUDA = "cuda:0"
def init_dls():
"""
Initializes DataLoader objects.
"""
train_data = CIFAR_10.train_data
test_data = CIFAR_10.test_data
train_dl = torch.utils.data.DataLoader(dataset = train_data,
batch_size = BATCH_SIZE,
shuffle = True)
test_dl = torch.utils.data.DataLoader(dataset = test_data,
batch_size = BATCH_SIZE,
shuffle = True)
return train_dl, test_dl
def train(model, train_dl, stepper):
"""
Trains models.
"""
for i in range(N_EPOCHS):
for inputs, outputs in train_dl:
results = model(inputs.to(CUDA))
stepper.zero_grad()
ERROR(results, outputs.to(CUDA)).backward()
stepper.step()
def accuracy(model, dl):
"""
Determines model accuracies for given DataLoader objects.
"""
n_correct = 0
for inputs, outputs in dl:
results = torch.max(model(inputs.to(CUDA)), 1)[1]
n_correct += (results == outputs.to(CUDA)).sum().item()
return 100 * n_correct / len(dl.dataset)
train_dl, test_dl = init_dls()
model = torch.hub.load("pytorch/vision",
"alexnet",
weights = "DEFAULT")
model.classifier[6] = torch.nn.Linear(4096, 10)
model.to(CUDA)
stepper = torch.optim.SGD(model.parameters(),
lr = LEARN_RATE,
momentum = MOMENTUM)
train(model, train_dl, stepper)
print(f"training accuracy: %{accuracy(model, train_dl)}")
print(f"testing accuracy: %{accuracy(model, test_dl)}")
Here is CIFAR_10.py:
import torchvision
import torchvision.transforms
TRAIN_FOL = "./train_data"
TRAIN_MEANS = [0.49139968, 0.48215841, 0.44653091]
TRAIN_STDS = [0.24703223, 0.24348513, 0.26158784]
TEST_FOL = "./test_data"
TEST_MEANS = [0.49421428, 0.48513139, 0.45040909]
TEST_STDS = [0.24665252, 0.24289226, 0.26159238]
train_trans = [torchvision.transforms.Resize(256),
torchvision.transforms.CenterCrop(224),
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(mean = TRAIN_MEANS,
std = TRAIN_STDS)]
train_trans = torchvision.transforms.Compose(train_trans)
train_data = torchvision.datasets.CIFAR10(root = TRAIN_FOL,
train = True,
transform = train_trans,
download = True)
test_trans = [torchvision.transforms.Resize(256),
torchvision.transforms.CenterCrop(224),
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(mean = TEST_MEANS,
std = TEST_STDS)]
test_trans = torchvision.transforms.Compose(test_trans)
test_data = torchvision.datasets.CIFAR10(root = TEST_FOL,
train = False,
transform = test_trans,
download = True)
Here are sample results:
Downloading https://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz to ./train_data/cifar-10-python.tar.gz 100%|██████████| 170498071/170498071 [00:01<00:00, 101605340.72it/s] Extracting ./train_data/cifar-10-python.tar.gz to ./train_data Downloading https://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz to ./test_data/cifar-10-python.tar.gz 100%|██████████| 170498071/170498071 [00:01<00:00, 91944695.56it/s] Extracting ./test_data/cifar-10-python.tar.gz to ./test_data Downloading: "https://github.com/pytorch/vision/zipball/main" to /root/.cache/torch/hub/main.zip Downloading: "https://download.pytorch.org/models/alexnet-owt-7be5be79.pth" to /root/.cache/torch/hub/checkpoints/alexnet-owt-7be5be79.pth 100%|██████████| 233M/233M [00:01<00:00, 231MB/s] training accuracy: %96.184 testing accuracy: %88.74
Fully connected layers are layers that correspond to Ai + b where i is the input, A is a matrix, and, b is a vector. These are also referred to as linear functions.
Sets of numbers have three quartiles, the medians and the medians of each half.
The following implements a PyTorch image classifier using the CIFAR 10 (Canadian Institute For Advanced Research) dataset:
import torch
import torch.nn
import CIFAR_10
N_CLASSES = 10
LEARN_RATE = 0.001
MOMENTUM = 0.9
BATCH_SIZE = 64
N_EPOCHS = 20
ERROR = torch.nn.CrossEntropyLoss()
class CNN(torch.nn.Module):
"""
Defines a convolutional neural network.
"""
def __init__(self, N_CLASSES):
super(CNN, self).__init__()
self.conv_1 = torch.nn.Conv2d( 3, 32, 3)
self.conv_2 = torch.nn.Conv2d(32, 32, 3)
self.pool_1 = torch.nn.MaxPool2d(2, stride = 2)
self.conv_3 = torch.nn.Conv2d(32, 64, 3)
self.conv_4 = torch.nn.Conv2d(64, 64, 3)
self.pool_2 = torch.nn.MaxPool2d(2, stride = 2)
self.line_1 = torch.nn.Linear(1600, 128)
self.relu_1 = torch.nn.ReLU()
self.line_2 = torch.nn.Linear(128, N_CLASSES)
def forward(self, inputs):
results = inputs
for f in [self.conv_1,
self.conv_2,
self.pool_1,
self.conv_3,
self.conv_4,
self.pool_2]:
results = f(results)
results = results.reshape(results.size(0), -1)
for f in [self.line_1, self.relu_1, self.line_2]:
results = f(results)
return results
def init_dls():
"""
Initializes DataLoader objects.
"""
train_data = CIFAR_10.train_data
test_data = CIFAR_10.test_data
train_dl = torch.utils.data.DataLoader(dataset = train_data,
batch_size = BATCH_SIZE,
shuffle = True)
test_dl = torch.utils.data.DataLoader(dataset = test_data,
batch_size = BATCH_SIZE,
shuffle = True)
return train_dl, test_dl
def train(model, train_dl, stepper):
"""
Trains models.
"""
for i in range(N_EPOCHS):
for inputs, outputs in train_dl:
results = model(inputs)
stepper.zero_grad()
ERROR(results, outputs).backward()
stepper.step()
def accuracy(model, dl):
"""
Determines model accuracies for given DataLoader objects.
"""
n_correct = 0
for inputs, outputs in dl:
results = torch.max(model(inputs), 1)[1]
n_correct += (results == outputs).sum().item()
return 100 * n_correct / len(dl.dataset)
train_dl, test_dl = init_dls()
model = CNN(N_CLASSES)
stepper = torch.optim.SGD(model.parameters(),
lr = LEARN_RATE,
momentum = MOMENTUM)
train(model, train_dl, stepper)
print(f"training accuracy: %{accuracy(model, train_dl)}")
print(f"testing accuracy: %{accuracy(model, test_dl)}")
Here is CIFAR_10.py:
import torchvision
import torchvision.transforms
TRAIN_FOL = "./train_data"
TRAIN_MEANS = [0.49139968, 0.48215841, 0.44653091]
TRAIN_STDS = [0.24703223, 0.24348513, 0.26158784]
TEST_FOL = "./test_data"
TEST_MEANS = [0.49421428, 0.48513139, 0.45040909]
TEST_STDS = [0.24665252, 0.24289226, 0.26159238]
train_trans = [torchvision.transforms.Resize((32,32)),
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(mean = TRAIN_MEANS,
std = TRAIN_STDS)]
train_trans = torchvision.transforms.Compose(train_trans)
train_data = torchvision.datasets.CIFAR10(root = TRAIN_FOL,
train = True,
transform = train_trans,
download = True)
test_trans = [torchvision.transforms.Resize((32,32)),
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(mean = TEST_MEANS,
std = TEST_STDS)]
test_trans = torchvision.transforms.Compose(test_trans)
test_data = torchvision.datasets.CIFAR10(root = TEST_FOL,
train = False,
transform = test_trans,
download = True)
Here are sample results:
Downloading https://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz to ./train_data/cifar-10-python.tar.gz 100.0% Extracting ./train_data/cifar-10-python.tar.gz to ./train_data Downloading https://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz to ./test_data/cifar-10-python.tar.gz 100.0% Extracting ./test_data/cifar-10-python.tar.gz to ./test_data training accuracy: %85.46 testing accuracy: %68.43
Convolutional neural networks are artificial neural networks with layer convolutions. Our eyes function similarly to convolutional neural networks. A famous example is AlexNet.
The convolution of functions f and g is defined as follows:
The cross correlation of functions f and g is defined as follows:
Transfer learning is supervised learning that uses existing models. Fine tuning is a transfer learning method which modifies existing models using new data. Other methods use existing models unchanged to transform inputs to new models.
Classification providing probabilities for all categories is referred to as probabilistic classification.
Data augmentation is adding transformed versions to data. Examples include adding scaled, cropped, flipped and rotated versions to image sets.
In classification models, with softmax results, logits are the softmax inputs.
Artificial narrow intelligence (ANI) software imitates limited aspects of intelligence such as chess programs. Artificial general intelligence (AGI) software imitates most aspects of intelligence such as many science fiction programs. Artificial super intelligence (ASI) software imitates behaviors that surpass most aspects of intelligence.
Active learning methods are interactive supervised learning labeling methods that try to minimize the amount of labeling.
Data wrangling is data preparation.
Data cubes are arrays.
Markov decision processes are action event sequences where:
Agents perform actions in environments.
Actions lead to state transitions and rewards.
Final state probabilities for all action initial state pairs are known.
Rewards for all action state transition pairs are known.
Final state probabilities and rewards depend only on present states and not past states.
Many problems are finding Markov decision process actions that maximize expected total rewards. Examples include developing chess and traffic light strategies.
Markov chains are event sequences where event probabilities depending only on present states and not past states. Examples include Brownian motion and next word predictions.
Reinforcement learning methods automate the creation of programs that maximize rewards. Agents in environments have trial and error sessions:
Transactional databases optimize for low data reading and writing. Analytical databases optimize for high data reading. Analytical databases have high redundancy. Both database types are often used together.
Matplotlib is a low level plotting application. Seaborn is a high level plotting application built on Matplotlib. Plotly is a high level interactive plotting application. Dash is a dashboard application built on Plotly.
Principal components are eigenvectors of covariant matrices. Eigenvalues of principal components denote importance.
Covariance matrices contain covariances which are functions of two sets:
Pandas Timestamp objects denote dates and times in nanoseconds with 64 bit integers. The implies about a 584 year range. Therefore, Pandas cannot represent dates and times before 1677-09-22T00:12:43.145225 or after 2262-04-11T23:47:16.854775807.
Estimators are model builders.
Summary statistics summarize data. They often include counts, minima, maxima, means, medians, modes, standard deviations, variances and interquartile ranges.
Dummies are one hot encoding bits.
Mean absolute errors are error absolute value averages.
Root mean square errors are residual root mean squares.
Features are properties.
Loss functions define model result errors.
Bidirectional recurrent neural networks combine the results of two recurrent neural networks where one receives the inputs in reverse order.
Recurrent neural networks are stateful artificial neural networks where inputs modify states. Results depend on inputs as well as states.
Many classification models depend on whether certain probabilities are above certain minima. These minima are referred to as thresholds.
It is often useful to modify backpropagation method layer inputs so that each input element has an average of zero and a variance of one per training data subset. This process is referred to as batch normalization.
It is often useful in backpropagation method updates to include fractions of previous updates. These fractions are referred to as momenta.
Sensitivity (recall) corresponds to the fraction of positive values predicted. Specificity corresponds to the fraction of negative values predicted.
The fractions of values, along the diagonals of confusion matrices, correspond to accuracy.
Correlation coefficients denote the linearity in relations between two variables. Correlation matrices contain multiple correlation coefficients:
Scatter plot matrices contain multiple scatter plots:
Dropout is a backpropagation method regularization technique. It involves ignoring randomly selected function values.
Imputation is the process of replacing missing values in datasets by inferences from the present values.
Backpropagation method updates can be applied per training subset. These training subsets are referred to as batches. Smaller batch sizes typically lead to greater model accuracies.
Random forest methods are decision tree methods that use bootstrapping.
Decision tree methods create flowchart models.
Box Cox transformations, (xᵏ - 1) / k, make frequency distributions closer to normal distributions for 0 < k < 1. They are equivalent to log(x) in the limit as k approaches 0. These transformations are also referred to as power transformations.
Bootstrapping is an ensemble method using models built from random input output pair selections. The collections may contain duplicates and be overlapping. Bootstrapping is also referred to as bagging.
Logistic regression is a classification method using the logistic function:
The softmax function turns vectors into ones with components that add up to one. They are often used in machine learning models where results are probabilities:
Pie charts denote compositions of entities. Stacked bar charts denote compositions of multiple entities:
Scatter plots denote relations between two variables. Bubble charts denote relations between three variables:
Histograms denote variable value interval frequencies. Bar charts denote variable values.
Box plots are formed from quartiles and extrema:
Confidence scores are probabilities of model results being correct.
Incremental learning is building new supervised learning models from existing ones using new training data.
Object standardization is the process of replacing words, in texts, that are not found in dictionaries. These include slang, abbreviations and acronyms.
Both oversampling and undersampling are processes that modify sets to alter proportions of element types. Oversampling methods may involve adding exact or modified copies of elements that are randomly selected. Undersampling methods may involve removing elements that are randomly selected or selected using k means clustering.
Both sensitivity and true positive rate are other terms for recall.
Stop words are common words that are ignored in machine learning.
Type 1 errors are false positives. Type 2 errors are false negatives.
Both stemming and lemmatization are processes that remove word variations in texts. Stemming provides greater performance by ignoring word contexts. Lemmatization provides greater accuracy but analyzing word contexts.
Residuals are regression model prediction errors.
Variances are averages of squared deviations from averages. Standard deviations are square roots of variances.
Word2vec is a set of techniques to convert words into vectors such that closeness corresponds to semantic similarity. Word2vec relies on the observation that semantically similar words tend to occur near the same other words in texts.
K means clustering divides vector sets into subsets based on distance. Consider distances from corresponding subset averages. K means clustering minimizes the sums of the squares of these distances.
F1 scores are the harmonic means of precision and recall values. F1 scores are equal to twice the ratios of products and sums. Macro F1 scores are F1 score averages.
The fractions of values that are correct, in rows and columns of confusion matrices, correspond to precision and recall. Precision depends on the number of false positives. Recall depends on the number of false negatives.
Confusion matrices give information about classification testing results:
Comparing supervised learning training and testing results from different data subsets is referred to as cross validation.
Term frequency-inverse document frequencies estimate the importance of words in documents. These estimates grow with word frequencies in documents, but, decrease with word frequencies in other documents. Estimates are often presented in matrices where rows and columns correspond to documents and terms respectively.
The number of standard deviations an element of a set differs from the average is referred to as its z score. An alternative to min max normalization is to replace numbers with z scores. This is referred to as standardization.
The Cartesian product of sets A and B is {(x, y) : x ϵ A and y ϵ B}.
Lists of words and word frequencies in text data are referred to as bags of words. Lists of phrases, up to some maximum word count, in text data are referred to as n-grams.
Converting a set of strings to a set of integers establishes an ordering. Converting a set of strings to a set of perpendicular unit vectors does not establish an ordering. This is referred to as one hot encoding.
Inference is the process of using supervised learning models.
Validation data are used to evaluate supervised learning method variations. Testing data are used to evaluate supervised learning models. Often training, validation and testing data are 80%, 10% and 10% respectively of all the data.
AutoML is a Google service which creates programs using machine learning methods. For example, it can create an image classifier given a large set of categorized images.
Regularization is the use of techniques to avoid overfitting in supervised learning. A common backpropagation method regularization technique is to adjust the error function to penalize large weights and biases more. L1 (Lasso) regularization adds a term containing the sum of the absolute values of all the weights and biases. L2 (Ridge) regularization adds a term containing the sum of the squares of all the weights and biases.
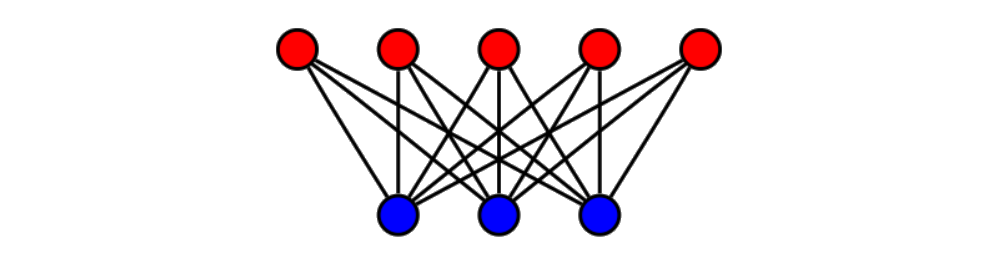
The backpropagation method is an extension of the perceptron method for acyclic artificial neural networks. Acyclic artificial neural networks are defined in terms of the following:
functions f1, f2, f3, ..., fN
weight matrices W1, W2, W3, ..., WN
bias vectors b1, b2, b3, ..., bN
such that the result for an input vector i involves:
o0 = i
oj = (fj (aj1), fj (aj2), fj (aj3), ..., fj (ajN)) for j = 1, 2, 3, ..., N
aj = Wj oj -1 + bj for j = 1, 2, 3, ..., N
where oN is the result.
In the backpropagation method, each weight matrix and bias vector is updated for each input output vector pair (i, o) by subtracting a small fraction of the corresponding partial derivative of the error function Eo = (o - oN)2 / 2. The small fraction is referred to as the learning rate. For a derivation of the formulas to calculate these partial derivatives, click here.
Here is sample Python backpropagation method code:
#!/usr/bin/env python3
"""
Implements the backpropagation method.
Usage:
./backprop <data file> \
<data split> \
<number of hidden layers> \
<number of hidden layer functions> \
<number of categories> \
<learning rate> \
<number of epochs>
Data files must be space delimited with one input output pair per line.
Every hidden layer has the same number of functions.
The hidden layer functions are rectified linear unit functions.
The outer layer functions are identity functions.
initialization steps:
The input output pairs are shuffled and the inputs mix max normalized.
The weights and biases are set to random values.
Requires NumPy.
"""
import numpy
import sys
def min_max(data):
"""
Finds the min max normalizations of data.
"""
return (data - numpy.min(data)) / (numpy.max(data) - numpy.min(data))
def init_data(data_file, data_split, n_cat):
"""
Creates the training and testing data.
"""
data = numpy.loadtxt(data_file)
numpy.random.shuffle(data)
data[:, :-1] = min_max(data[:, :-1])
outputs = numpy.identity(n_cat)[data[:, -1].astype("int")]
data = numpy.hstack((data[:, :-1], outputs))
data_split = int((data_split / 100) * data.shape[0])
return data[:data_split, :], data[data_split:, :]
def accuracy(data, weights, biases, n_cat):
"""
Calculates the accuracies of models.
"""
results = model(data[:, :-n_cat], weights, biases)
outputs = numpy.argmax(data[:, -n_cat:], 1)
return 100 * (results == outputs).astype(int).mean()
def model_(inputs, weights, biases, relu = True):
"""
model helper function
"""
results = numpy.matmul(weights, inputs.T).T + biases
if relu:
results = numpy.maximum(results, 0)
return results
def model(inputs, weights, biases):
"""
Finds the model results.
"""
results = model_(inputs, weights[0], biases[0])
for e in zip(weights[1:-1], biases[1:-1]):
results = model_(results, e[0], e[1])
results = model_(results, weights[-1], biases[-1], False)
results = numpy.argmax(results, 1)
return results
def adjust(weights, biases, input_, output, func_inps, func_outs, learn_rate):
"""
Adjusts the weights and biases.
"""
d_e_f_i = [func_outs[-1] - output]
d_e_w = [numpy.outer(d_e_f_i[-1], func_outs[-2])]
for i in reversed(range(len(weights) - 1)):
func_deriv = numpy.clip(numpy.sign(func_inps[i]), 0, 1)
vector = numpy.matmul(weights[i + 1].T, d_e_f_i[-1])
func_out = func_outs[i - 1] if i else input_
d_e_f_i.append(numpy.multiply(vector, func_deriv))
d_e_w.append(numpy.outer(d_e_f_i[-1], func_out))
for i, e in enumerate(reversed(list(zip(d_e_w, d_e_f_i)))):
weights[i] -= learn_rate * e[0]
biases[i] -= learn_rate * e[1]
def learn(train_data, n_hls, n_hl_funcs, n_cat, learn_rate, n_epochs):
"""
Learns the weights and biases from the training data.
"""
weights = [numpy.random.randn(n_hl_funcs, train_data.shape[1] - n_cat)]
for i in range(n_hls - 1):
weights.append(numpy.random.randn(n_hl_funcs, n_hl_funcs))
weights.append(numpy.random.randn(n_cat, n_hl_funcs))
weights = [e / numpy.sqrt(e.shape[0]) for e in weights]
biases = [numpy.random.randn(n_hl_funcs) for i in range(n_hls)]
biases.append(numpy.random.randn(n_cat))
biases = [e / numpy.sqrt(e.shape[0]) for e in biases]
for i in range(n_epochs):
for e in train_data:
input_ = e[:-n_cat]
func_inps = []
func_outs = []
for l in range(n_hls + 1):
input__ = func_outs[l - 1] if l else input_
func_inp = numpy.matmul(weights[l], input__)
func_inp += biases[l]
relu = numpy.maximum(func_inp, 0)
func_out = relu if l != n_hls else func_inp
func_inps.append(func_inp)
func_outs.append(func_out)
adjust(weights,
biases,
e[:-n_cat],
e[-n_cat:],
func_inps,
func_outs,
learn_rate)
return weights, biases
n_cat = int(sys.argv[5])
train_data, test_data = init_data(sys.argv[1], float(sys.argv[2]), n_cat)
weights, biases = learn(train_data,
int(sys.argv[3]),
int(sys.argv[4]),
n_cat,
float(sys.argv[6]),
int(sys.argv[7]))
print(f"weights and biases: {weights}, {biases}")
accuracy_ = accuracy(train_data, weights, biases, n_cat)
print(f"training data accuracy: {accuracy_:.2f}%")
accuracy_ = accuracy(test_data, weights, biases, n_cat)
print(f"testing data accuracy: {accuracy_:.2f}%")
Here are sample results for the MNIST dataset (Modified National Institute Of Standards And Technology dataset) available from many sources such as Kaggle:
./backprop MNIST_dataset 80 2 64 10 0.001 100
weights and biases: [array([[ 0.20884894, -0.02542065, -0.10987643, ..., -0.15665534,
-0.08775792, 0.0638999 ],
[-0.00592018, 0.18332229, -0.01387026, ..., 0.06527793,
0.13211286, 0.09518377],
...
0.00713001, -0.402518 , 0.21595368, 0.3279246 , -0.02778006,
0.01107208, 0.03471949, -0.27601775, -0.21284684, -0.1401997 ,
-0.20863759, -0.05693757, 0.09183485, -0.06464501]), array([-0.01450932, -0.00257944, -0.02661391, 0.026662 , -0.01042119,
-0.04099369, 0.66813539, 0.50147859, -0.08111961, -0.0198442 ])]
training data accuracy: 98.15%
testing data accuracy: 96.43%
Here is a plot of the accuracy versus the number of epochs for a data split of 80 / 20, two hidden layers, 64 functions per hidden layer, 10 categories, and, a learning rate of 0.001. Blue denotes the training data accuracy and orange denotes the testing data accuracy:
Feedforward artificial neural networks are acyclic artificial neural networks.
The rectified linear unit is a popular artificial neural network function. It is widely used in deep learning and is also referred to as the ramp function:
Deep learning methods are artificial neural network supervised learning methods involving large numbers of compositions of functions.
Supervised learning inputs are also referred to as samples.
Supervised learning outputs are also referred to as targets, classes and categories.
"The Navy revealed the embryo of an electronic computer today that it expects will be able to walk, talk, see, write, reproduce itself and be conscious of its existence." — New York Times, July 8, 1958
The perceptron method is one of the earliest and simplest artificial neural network supervised learning methods. It involves the single function H(w · i + b) where H is the Heaviside step function and i is the input. w and b are referred to as the weights and the bias. For every input output pair (i, o), a scaled version of i is added to w, and, the scale factor of i is added to b. The scale factor for every i is γ(o - H(w · i + b)) for some small γ referred to as the learning rate.
Here is sample Python perceptron method code:
#!/usr/bin/env python3
"""
Implements the perceptron method.
Usage:
./perceptron <data file> <data split> <learning rate> <number of epochs>
Data files must be space delimited with one input output pair per line.
initialization steps:
Input output pairs are shuffled.
Inputs are min max normalized.
Weights are set to random values.
Requires NumPy.
"""
import numpy
import sys
def min_max(data):
"""
Finds the min max normalizations of data.
"""
return (data - numpy.min(data)) / (numpy.max(data) - numpy.min(data))
def init_data(data_file, data_split):
"""
Creates the training and testing data.
"""
data = numpy.loadtxt(data_file)
numpy.random.shuffle(data)
data[:, :-1] = min_max(data[:, :-1])
ones = numpy.ones(data.shape[0])[None].T
data = numpy.hstack((data[:, :-1], ones, data[:, -1][None].T))
data_split = int((data_split / 100) * data.shape[0])
return data[:data_split, :], data[data_split:, :]
def accuracy(data, weights):
"""
Calculates the accuracies of models.
"""
model_ = model(data[:, :-1], weights)
return 100 * (model_ == data[:, -1]).astype(int).mean()
def model(inputs, weights):
"""
Finds the model results.
"""
return (numpy.matmul(inputs, weights) > 0).astype(int)
def learn(data, learn_rate, n_epochs):
"""
Learns the weights from data.
"""
weights = numpy.random.rand(data.shape[1] - 1) / (data.shape[1] - 1)
for i in range(n_epochs):
for e in data:
model_ = model(e[:-1], weights)
weights += learn_rate * (e[-1] - model_) * e[:-1]
return weights
train_data, test_data = init_data(sys.argv[1], int(sys.argv[2]))
weights = learn(train_data, float(sys.argv[3]), int(sys.argv[4]))
print(f"weights and bias: {weights}")
print(f"training data accuracy: {accuracy(train_data, weights):.2f}%")
print(f"testing data accuracy: {accuracy(test_data, weights):.2f}%")
Here are sample results for a subset of the popular MNIST dataset (Modified National Institute Of Standards And Technology dataset) available from many sources such as Kaggle. Results denote whether the inputs correspond to the number eight or not:
% ./perceptron MNIST_subset_dataset 80 0.000001 100 weights and bias: [ 9.60835270e-04 7.78817831e-04 9.09208513e-04 1.23811178e-04 1.24167654e-03 6.78889421e-04 5.61003207e-04 6.95360517e-04 7.41301570e-04 7.99198618e-04 5.40027576e-04 1.53847709e-05 6.85229222e-04 7.34466515e-04 1.10555270e-03 3.54355472e-04 ... 3.49190104e-04 9.08839645e-04 2.15854858e-04 7.85936614e-04 2.48270482e-04 7.91941436e-04 5.33470893e-04 4.43331643e-04 9.53736704e-04 2.42570411e-04 9.22297554e-04 9.67634113e-04 -1.70084762e-03] training data accuracy: 89.75% testing data accuracy: 86.32%
Here is a plot of the accuracy versus the number of epochs for a data split of 80 / 20 and a learning rate of 0.000001. Blue denotes the training data accuracy and orange denotes the testing data accuracy:
Hyperparameters specify machine learning method variations
Artificial neural networks (ANNs) are function compositions which correspond to idealized neural networks. The functions are referred to as layers.
Ensemble methods involve multiple machine learning methods.
Min max normalizations transform sets of numbers into ones with the extrema zero and one. Let m and M denote the minimum and maximum of a set of numbers. The min max normalization of that set replaces every element x with (x - m) / (M - m).
Models are function approximations created with supervised learning methods.
Epochs are supervised learning steps which process all of the input output pairs.
Using supervised learning methods to approximate piecewise constant functions is referred to as classification. Using supervised learning methods to approximate continuous functions is referred to as regression.
Training data are supervised learning input output pair sets.
Modes are the most frequent elements of sets.
The k nearest neighbors method is one of the simplest supervised learning methods. It involves finding the most similar inputs in the set of input output pairs.
Here is sample Python code to determine the accuracy of the k nearest neighbors method on data:
#!/usr/bin/env python3
"""
Determines the accuracy of the k nearest neighbors method on data.
Usage:
./k_nn <data file> <data split> <number of nearest neighbors>
Data files must be space delimited with one input output pair per line.
initialization steps:
Input output pairs are shuffled.
Inputs are min max normalized.
Requires SciPy and NumPy.
"""
import scipy.stats
import numpy
import sys
def min_max(data):
"""
Finds the min max normalizations of data.
"""
return (data - numpy.min(data)) / (numpy.max(data) - numpy.min(data))
def init_data(data_file, data_split):
"""
Creates the model and testing data.
"""
data = numpy.loadtxt(data_file)
numpy.random.shuffle(data)
data[:, :-1] = min_max(data[:, :-1])
data_split = int((data_split / 100) * data.shape[0])
return data[:data_split, :], data[data_split:, :]
def accuracy(model_data, test_data, n_nn):
"""
Calculates the accuracies of models.
"""
model_ = model(test_data[:, :-1], model_data, n_nn)
return 100 * (model_ == test_data[:, -1]).astype(int).mean()
def model_(input_, model_data, n_nn):
"""
model helper function
"""
squares = (input_ - model_data[:, :-1]) ** 2
indices = numpy.sum(squares, 1).argsort()[:n_nn]
return scipy.stats.mode(numpy.take(model_data[:, -1], indices))[0][0]
def model(inputs, model_data, n_nn):
"""
Finds the model results.
"""
return numpy.apply_along_axis(lambda e : model_(e, model_data, n_nn),
1,
inputs)
model_data, test_data = init_data(sys.argv[1], float(sys.argv[2]))
n_nn = int(sys.argv[3])
print(f"testing data accuracy: {accuracy(model_data, test_data, n_nn):.2f}%")
Here are sample results for the popular Iris flower dataset available from many sources such as Scikit-learn:
% ./k_nn Iris_flower_dataset 80 1 testing data accuracy: 96.67% % ./k_nn Iris_flower_dataset 80 2 testing data accuracy: 93.33%
Symbol manipulation can correspond to thinking. Therefore, computers can correspond to minds and replace humans at some mental tasks.
Underfitting is the creation of supervised learning continuous function approximations that are too simple. Overfitting is the creation of supervised learning continuous function approximations that are too complex. Both decrease accuracy.
NumPy arrays are a fundamental data structure of machine learning with Python. Pandas, SciPy, Scikit-learn and many other libraries use Numpy arrays.
Labeled means categorized. Supervised learning methods require labeled inputs.
Statistics is a superset of what is often referred to as data science. The field of statistics predates computers.
Supervised learning methods automate the creation of programs that approximate functions. They require input output pairs.
Intelligence does not have a rigorous definition. Rather than trying to define intelligence, Alan Turing suggested trying to create devices that act as if they have intelligence. Quality can be measured by their ability to fool people.
Computers are symbol manipulation machines.
Machine learning methods automatically create programs. They are useful when creating programs is inconvenient, impractical or even impossible for humans. Many inventions surpass humans in limited ways. Cars move faster than humans. Cranes lift more than humans. Calculators calculate better than humans. Now an invention surpasses humans at programming!